2024年省考行测备考技巧干货：混合增长率终极技巧讲解

　　同学们，在公职类考试中，都会遇到混合增长率的题目，这一类题目都属于技巧类题目，很多题是需要计算即可判定出答案，但是有些同学在做题的时候，又发现这个混合增长率的判定法则好像不太适用所有的题目，觉得做题还是要硬算，但是硬算(常规计算)的话又太费时间，所以把这一类的题目放弃了。

　　这种的观点是错误的，在公考中，任何一种方法和技巧都是有用的，每一分我们都要争取，那么现在将混合增长率的判定技巧给同学们进行深入讲解。

　　首先，我们先回顾混合增长率的判定结论：1.整体的增长率大于部分中最小的增长率，小于部分中最大的增长率。(R最小

　　增长率=增长量/基期量是，我们初中在学习化学的时候有一个公式：浓度=溶质/溶液，生活中常见例子就是糖水浓度=糖/糖水。由于两个公式本质是一样的，所以我们可以做类比推理：

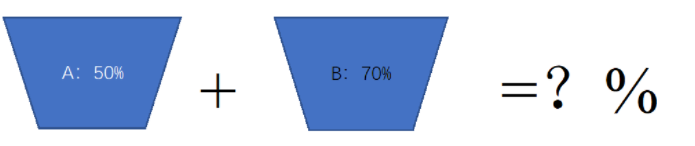
　　大家可以看上图，我们有两个烧杯，一杯糖水浓度50%，一杯糖水浓度70%，将两杯糖水倒在一起，新的糖水浓度是多少?同学们肯定会说，新的糖水浓度在50%-70%之间。那如果我们换成三杯呢?

　　大家可以看上图，如果我们烧杯的数量变成了三个，A,B,C浓度不一致，这个时候，有同学就会说，老师三杯也是一样的道理，我们三杯倒在一起，新糖水的浓度在20%-70%之间，那好了，大家想一想如果是四杯，五杯是不是一样的原理，混合后的浓度大于其中最小的，小于其中最大的。那么我们第一个混合增长率的结论就推导出来了：：1.整体的增长率大于部分中最小的增长率，小于部分中最大的增长率。(R最小

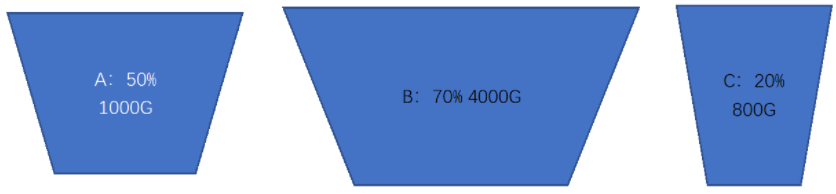
　　从上图我们可以发现，三个烧杯都被我赋予了质量，50%浓度的有1000G，70%浓度的有4000G，20%有800G，那么这时候我问同学们，混合后的糖水会偏向于哪一个浓度，这个时候同学们肯定会说偏向于70%因为它的杯子大。那这就是我们第二个推论了：2.整体增长率偏向于基期量较大的一方。

　　有了结论之后，我们做题就方便了，比如我们看一下下面的例题：

　　例1：某市2021年上半年GDP的增长率为20%，2020年上半年GDP为1000亿元，2021年下半年GDP的增长率为50%，2020年下半年GDP为500亿元。问该市2021年全年的GDP增长率最接近()

　　A.22% B.19% C.55% D.48%

　　同学们，可以看上面一道题，我们全年可以分为上半年和下半年，所以全年的增长率介于20%-50%之间，那么我们可以排除BC了，又因为偏向于基期量较大的一方，所以1000亿元和500亿元做比较，这时候大家就之道选A了。

　　例1比较简单，但是很多同学遇到例2就蒙了。

　　例2：某市2021年上半年GDP的增长率为20%，2020年上半年GDP为1000亿元，2021年下半年GDP的增长率为50%，2020年下半年GDP为500亿元。问该市2021年全年的GDP增长率最接近()

　　A.22% B.35% C.28% D.33%

　　遇到例2，同学们可能就蒙了，根据混增原理，我们只能判定其在20%-50%之间，但是无法判定具体的数值，那是不是就要根据已知条件硬算呢?其实，这种题才是同学们的难点，那么考试的时候如何去做，有没有速算的方法。我们下面看一看一个例子。

　　假如，我们有一杯A糖水30%的浓度，质量为100G，另外一杯B糖水45%，质量为200G，那么两杯糖水混合之后，新糖水的浓度是(30%✖100+45%✖200)/300=40%。这个是我们计算出来的结果，那么有没有比较简便的方法?

　　那么大家可以看一下，根据混增原理，新糖水的浓度在30%-45%之间，我们可以知道最后糖水浓度取决于两杯糖水的质量，那么我们可以转化为比例关系，大家看一下，A糖水的质量：B糖水的质量=1：2，30%-45%之间相差15%的浓度，那么说明我们糖水把15%浓度分成了3份，其中A占一份，B占两份，要使得它们最终混合后的浓度一致，是不是A要补齐两份，B要补齐一份。那么我们就可以知道了，新糖水的浓度是(30%+2✖5%)补足两份或(45%-1✖5%)补足一份，结果都是40%。所以我们可以用此结论去处理例题2。

　　结论3：一个整体被分成了两个部分，两个部分增长率的差值被均分成两个部分基期量比例和值份，整体的增长率等于其中任一一个部分的增长率加上比例数的反比份数。

　　根据例题2的描述，我们增长率在20%-50%之间，上半年的GDP：下半年的GDP=2：1，说明30%的增长率被分成了3份，所以根据结论3，我们可以推导出，2021年全年的GDP增长率为30%，所以答案选B。

　　混增原理是公考重要知识点，在考试之前，希望同学们能多练题，将其掌握。

（编辑：阿正）