近几年数量关系和资料分析模块的 考题中, 认真分析和观察可以归纳总结出一些出题的趋势和规律 ,下面就来总结一些数量和资料中的出题小规律。
【例1】
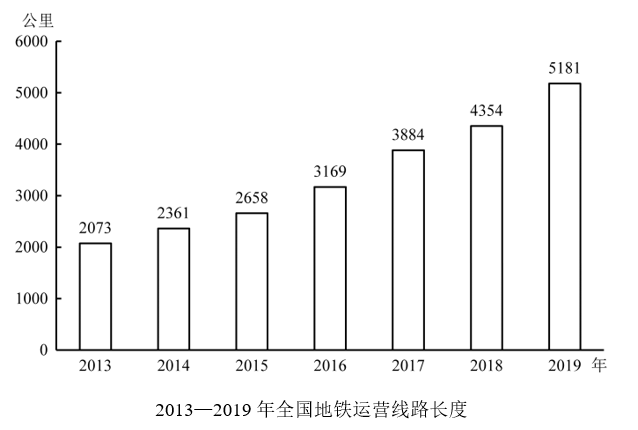
2014—2019年间,全国地铁运营线路长度同比增长20%以上的年份有几个?
A.1 B.2
C.3 D.4
【答案】A
【解析】第一步,本题考查增长率计算比较。
第二步,定位柱状图。
第三步,根据增长率=(现期量/基期量)-1,若要使增长率>20%,则现期量>基期量×1.2。代入数据可得:2014年2361<2073×1.2=2487.6,2015年2658<2361×1.2=2833.2,2016年3169<2658×1.2=3189.6,2017年3884>3169×1.2=3802.8,2018年4354<3884×1.2=4660.8,2019年5181<4354×1.2=5224.8,故同比增速超过20%的仅有2017年这1个年份。
因此,选择A选项。
【例 2 】
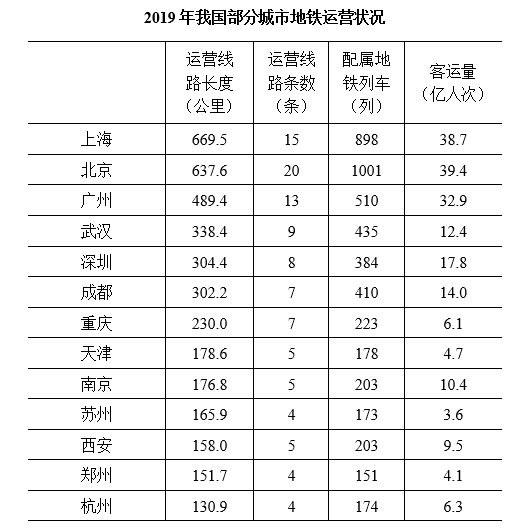
表中所列2019年地铁客运量超过10亿人次的城市中,2019年平均每条地铁运营线路长度超过40公里的城市有几个?
A.1 B.2
C.3 D.4
【答案】B
【解析】第一步,本题考查现期平均数比较。
第二步,定位表格材料。
第三步,直接读数可知,表中所列2019年地铁客运量超过10亿人次的城市有:上海(38.7亿人次)、北京(39.4亿人次)、广州(32.9亿人次)、武汉(12.4亿人次)、深圳(17.8 亿人次)、成都(14.0亿人次)、南京(10.4亿人次)。根据平均数=后/前=地铁运营线路长度/运营线路条数>40,即地铁运营线路长度>运营线路条数×40。可得,满足的有上海(669.5>15×40=600)、成都(302.2>7×40=280),共2个。
因此,选择B选项。
通过以上2个例题,可以发现 定值比较类的题 目特征为:问题中会 与 固定数值 进行比较且基础 比较方法为除法计算;做题方法 :将基础公式中的除法计算 转化为乘法计算,再进行比较 , 相对简单 。
其次,对于数量关系来说,近几年 在考查 几何问题 时容易和行程 问题相结合,在 2 020 年就有考查:
【例3】部队前哨站的雷达监测范围为100千米。某日前哨站侦测到正东偏北30° 100千米处,一架可疑无人机正匀速向正西方向飞行。前哨站通知正南方向150千米处的部队立即向正北方向发射无人机拦截,匀速飞行一段时间后,正好在某点与可疑无人机相遇。问我方无人机速度是可疑无人机的多少倍? A. B. C. √3+1 D. 3(√3-1)
【解析】 第一步,本题考查几何问题。
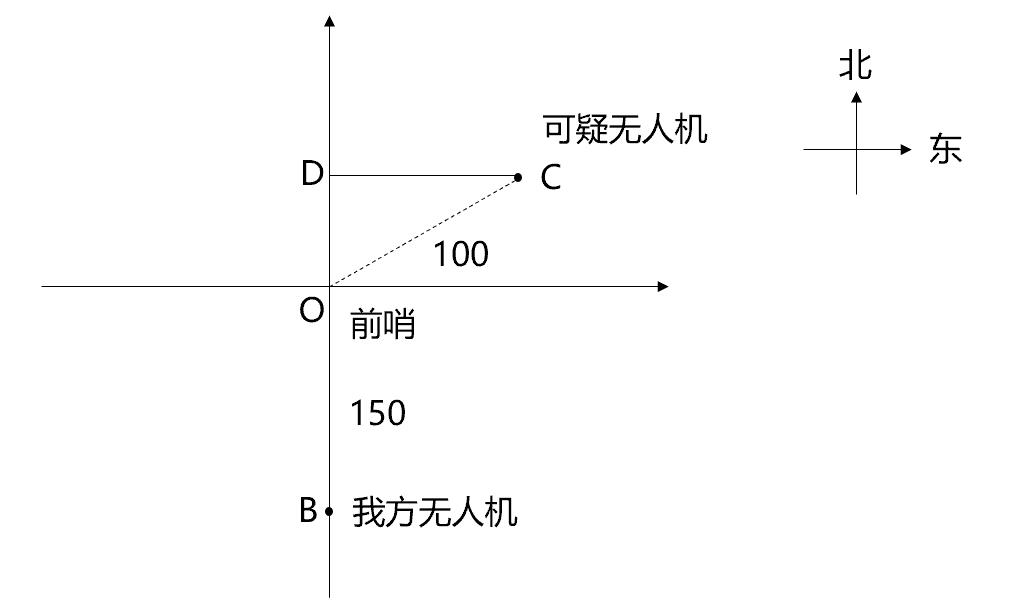
第二步,根据题意,我方无人机与可疑无人机相遇时,飞行距离如图所示: 我方无人机的飞行距离为BD=BO+OD,可疑无人机的飞行距离为CD,结合直角三角形的特性,OD=OC/2=50,CD=50 ,则BD=200。结合比例行程:时间一定的时候,速度与路程呈正比,则我方无人机的速度:可疑无人机的速度=BD:CD=200:50 = 。
因此,选择B选项。
通过上面例题可以发现,几何行程相结合的问题在做题的时候,一定要将图示准确画出来, 然后将几何的性质以及公式与行程问题的知识点相结合 再 进行做题,一般较多使用三角形相关性质和比例 行程 进行解题。