1.(单选题)商店采购了一种水果,第一天在进货成本基础上加价40%销售,从第二天开始,每天的销售价格都比前一天低10%。已知第三天这种水果的售价比第一天降低了13.3元/千克。问这种水果的进货成本为多少元/千克?
A.35
B.40
C.45
D.50
解析
第一步,本题考查经济利润问题。
第二步,设水果的进货成本为x元/千克,根据题意,则第一天的售价为1.4x元/千克,第三天的售价为1.4x×(1-10%)×(1-10%)=1.134x(元/千克),根据第三天比第一天降低13.3元/千克,可得1.4x-1.134x=13.3,解得x=50。
因此,选择D选项。
2.(单选题)为响应推动我国社会主义文化事业大发展大繁荣的号召,某小区决定为小区内每位老人准备40元文化基金,同时为每位儿童比老人多准备20元文化基金。已知该小区老人比儿童多100人,文化基金一共14000元,则该小区老人和儿童总数为:
A.300
B.320
C.360
D.480
解析
第一步,本题考查基础应用题。
第二步,设小区儿童为x人,则老人有(x+100)人,根据题意可得(40+20)x+40(x+100)=14000,解得x=100。
第三步,该小区老人和儿童总数为100+(100+100)=300(人)。
因此,选择A选项。
3.(单选题)在一个坡面角约为20°的山坡上有一个泉眼,从泉眼开挖一条正对山脚向下到山脚的灌溉水渠。已知泉眼距地面的垂直高度约为100米,开挖水渠每米的土方量约为0.3立方米,则开挖整条水渠的土方量约为。(sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
A.10立方米
B.32立方米
C.88立方米
D.980立方米
解析
第一步,本题考查几何问题中的平面几何类。
![]()
第二步,设泉眼到山脚的距离为x米,因为泉眼距地面的垂直高度约为100米,且sin20°≈0.34,可得,解得x约等于294米,又因为开挖水渠每米的土方量约为0.3立方米,则开挖整条水渠的土方量约为294×0.3=88.2立方米。
因此,选择C选项。
4.(单选题)某村拟建造一个容积为144立方米,深度为4米的长方体无盖蓄水池。经测算,蓄水池底部造价为260元/平方米,侧面造价为180元/平方米。那么该水池的最低总造价为:
A.11440元
B.25920元
C.26640元
D.31680元
解析
第一步,本题考查几何问题其他几何类。
![]()
第二步,蓄水池容积为144立方米,深度为4米,则蓄水池底面积为=36平方米,由于蓄水池底面积固定,若要总造价最低,则使得侧面积最小即可。根据几何性质,矩形面积固定,正方形周长最小,蓄水池底面边长为=6米时侧面积最小,侧面积为(6×4)×4=96平方米。
第三步,则总造价最低为36×260+96×180=26640元。
因此,选择C选项。
5.(单选题)某校师生为元旦晚会排练合唱表演,要求合唱团在台阶上排列成不少于3排的前多后少的梯形队阵,且各排的人数须是连续的自然数,以使后一排的合唱团成员均站在前一排两名合唱团成员之间的空隙处。若合唱团共100人,则满足上述要求的排列方案有( )种。
A.1
B.2
C.3
D.4
解析
第一步,本题考查数列问题。
![]()
第二步,根据等差数列的求和公式可知,,进一步整理可得200=(2+n-1)×n,n和n-1的奇偶性相反,则200要分解为一个奇数,一个偶数的乘积,且n小于前面的数。200=5×40=25×8,即第一种方式为,5排,第一排18人。第二种方式为,8排,第一排9人。共2种方式。
因此,选择B选项。
6.(单选题)某部门里身高各不相同的8人一起排练合唱节目。合唱要求8人排成两排,前后人员对齐,但要求后排的每个人要比站其前面的那个人高,以不被挡住。则这8人的站位方法有( )种。
A.980
B.1260
C.1860
D.2520
解析
第一步,本题考查排列组合问题。
![]()
第二步,将8人分为四列,每列2人,这2人站位情况仅1种。依次选出第一列至第四列,分别为:、、、,则这8人的站位方法有(种)。
因此,选择D选项。
7.(单选题)某水果批发商从果农那里以10元/公斤的价格购买了一批芒果,运送到某地区售出。在长途运输过程中有5%的芒果磕碰受损和另外5%的芒果过度成熟,因此无法卖出,其余部分以25元/公斤的价格售出后,如果不计运输等其他费用,这批芒果赚得利润12000元。则该批发商从果农那里购买了多少公斤芒果?
A.480
B.800
C.960
D.1000
解析
第一步,本题考查经济利润问题,属于基础公式类,用方程法解题。
第二步,设总共购买了x公斤芒果,总共卖出了90%,即0.9x,根据总售价=总成本+利润,可得25×0.9x=10×x+12000,解得x=960。
因此,选择C选项。
8.单选题)已知有6个大小相同,标号分别为1~6的正方形。若旋转后正方形编号相同算同一种拼法,那么要将这些木块拼成一个大长方形,有多少种不同的拼法?
A.360
B.540
C.720
D.900
解析
第一步,本题考查排列组合问题。
第二步,如下图所示,6个正方形组成一个长方形可以分为两种情况。
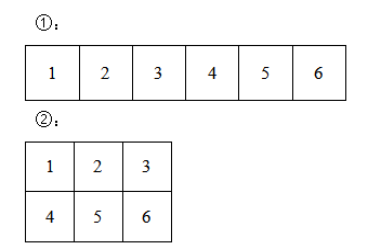
![]()
①6个数的排列方式有(种),但在一字排列中例如123456和654321这两种对称排列算一种拼法,则需要除以2去重复,则一字排列排法为720÷2=360(种)。
![]()
②当有两排时,第一排的排列方式有(种),第二排的排列方式有(种),但同①的道理也存在重复,因此排列方式有120×6÷2=360(种)。
第三步,排列方式共有360+360=720(种)。
因此,选择C选项。
9.(单选题)某医院门诊大楼最多容纳1500人,进出大楼有4个门,其中2个大门大小一致,2个小门大小一致。大楼安全员对4个的通行能力进行测试,同时打开1个大门和两个小门,2分钟内可通过600人;同时打开1个大门和1个小门,3分钟内可通过720人。当紧急情况发生时,出门效率降低30%。根据安全标准,紧急情况下大楼所有人员需在5分钟内撤离,那么发生紧急情况时这4个门最多能够通过多少人?
A.1440
B.1500
C.1600
D.1680
解析
解法一:
第一步,本题考查统筹推断。
第二步,设大门每分钟通过x人,小门每分钟通过y人,根据题意有:2(x+2y)=600,3(x+y)=720,解得x=180,y=60;则紧急情况下,5分钟内能够通过人数为(2×180+2×60)×5×(1-30%)=1680(人),然而整个门诊大楼最多容纳1500人,小于四个门能够通过的人数。
因此,选择B选项。
解法二:
第一步,本题考查统筹推断。
![]()
第二步,已知1个大门、1个小门3分钟通过720人,则可得2个大门、2个小门3分钟通过1440人,5分钟通过(人),紧急情况时,通过2400×(1-30%)=1680(人),然而整个门诊大楼最多容纳1500人,小于四个门能够通过的人数。
因此,选择B选项。
10.(单选题)某总公司由A、B、C三个分公司构成,若A公司的产出增加10%,可使总公司产出增加5%,若B公司产出增加10%,可使总公司产出增加2%,问若C公司产出减少10%可使总公司的产出减少百分之几?
A.2
B.3
C.4
D.5
解析
第一步,本题考查基础应用题。
![]()
第二步,赋值A、B、C三个分公司总产出为100,则A公司产出,B公司产出,故C公司产出100-50-20=30。
![]()
第三步,若C公司产出减少10%,可使总公司产出减少。
因此,选择B选项。