2022-04-07 13:31:10 甘肃公考考试网 //gs.huatu.com/gwy/
![]() 关注公众号领资料
关注公众号领资料
![]() QQ备考群
QQ备考群
![]() APP刷题
文章来源:华图教育
APP刷题
文章来源:华图教育
通常在题目中遇到计算不规则图形的面积时,首当其冲会选择采用割补法,将不规则的图形切割或者补充为较为基本的规则图形再进行计算,但有的时候割补后的规则图形面积往往计算起来相对比较繁杂,基本图形的面积直接相加或相减的方法并没有想象中那么简单。但是如果借助容斥原理来求解,另辟蹊径会变得非常简便。
【例1】
求图中阴影部分的面积。
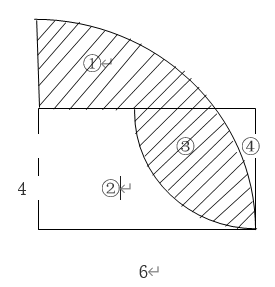
【解】并非所有的求解不规则阴影面积的题目都可以使用容斥原理进行解答,需要寻找阴影面积相互之间的关系与容斥原理进行类比,本题中阴影部分面积①+③=大扇形-②,
继续观察,②=长方形-小扇形的面积,可以求出②的面积,进一步可以解得阴影部分面积①+③。
大扇形=①+②+③
小扇形=③+④
长方形=②+③+④,
要求的是①+③=大扇形+小扇形-长方形
=[①+②+③]+[③+④]-[②+③+④]=①+③
【例2】求图中阴影部分的面积。
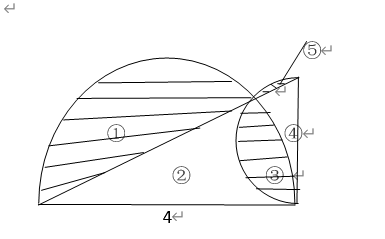
【解】大扇形=①+②+③,小扇形=③+④+⑤,三角形=②+③+④,
阴影部分面积=①+③+⑤=大扇形+小扇形-三角形
=[①+②+③]+[③+④+⑤]-[②+③+④]
