巧用赋值法求解给定时间型工程问题

　　在行测考试中，数量关系一直是比较难的模块，对于“菜鸟”而言就是噩梦一般，对于“高手”来说可能是制胜的法宝。其实，有些题型的解题方法是比较成熟的，也容易被广大考生所掌握。对于这类题目，想要上岸的考生非常有必要来充分理解并熟练运用。今天，华图教育就教给大家如何用赋值法求解给定时间型工程问题。

　　【题目特征】

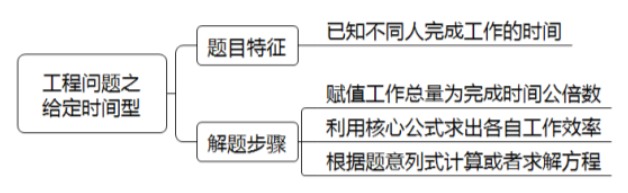
　　如果一道工程问题的已知条件是不同人完成工作的时间，那么它就属于给定时间型。

　　【解题步骤】

　　1、赋值工作总量为完成的时间的公倍数;

　　2、利用核心公式“工作总量=工作效率×工作时间”求出各自的工作效率;

　　3、根据题意列式计算或者求解方程。

　　【举个例子】

　　一项工作，如果甲单独完成需要2天，乙单独完成需要3天，求两人合作需要几天完成?

　　1、将工作总量赋值为6，即甲和乙单独完成工作的时间的公倍数;

　　2、根据公式：工作总量=工作效率×工作时间，可以求得甲的工作效率为6÷2=3，乙的工作效率为6÷3=2;

　　3、两人合作的效率为3+2=5，合作的时间为6÷5=1.2天。

　　下面我们来看几道例题：

　　【例题1】一项工程由甲、乙工程队单独完成，分别需50天和80天。若甲、乙工程队合作20天后，剩余工程量由乙、丙工程队合作需12天完成，则丙工程队单独完成此项工程

　　所需的时间是：

　　A. 40天 B. 45天

　　C. 50天 D. 60天

　　【答案】D。解析：已知条件为甲、乙工程队单独完成工作的时间，本题属于给定时间型。赋值工作总量为50和80的公倍数400，则甲工程队的效率为400÷50=8，乙工程队的效率为400÷80=5。若想求丙工程队单独完成此项工程所需的时间，需要求出丙工程队的效率。设丙工程队的效率为v，根据“若甲、乙工程队合作20天后，剩余工程量由乙、丙工程队合作需12天完成”，列出方程，20×(8+5)+12×(5+v)=400，解得v=，则丙工程队单独完成此项工程所需的时间是天。因此，选择D选项。

　　【例题2】手工制作一批元宵节花灯，甲、乙、丙三位师傅单独做，分别需要40小时、48小时、60小时完成。如果三位师傅共同制作4小时后，剩余任务由乙、丙一起完成，则乙在整个花灯制作过程中所投入的时间是( )。

　　A. 24小时 B. 25小时

　　C. 26小时 D. 28小时

　　【答案】A。解析：已知条件为甲、乙、丙单独完成工作的时间，本题属于给定时间型。赋值工作总量为40、48和60的公倍数240，则甲师傅的效率为240÷40=6，乙师傅的效率为240÷48=5，丙师傅的效率为240÷60=4。设剩余任务乙工作时间为t，根据“三位师傅共同制作4小时后，剩余任务由乙、丙一起完成”，列出方程，240=4×(6+5+4)+(5+4)×t，解得t=20，再加上三人合作的4小时，乙在整个花灯制作过程中所投入的时间为20+4=24小时。因此，选择A选项。

　　以上就是运用赋值法解决给定时间类工程问题的思路和方法，华图教育希望大家能够熟练掌握，成功上岸!

 

（编辑：干饭人）