绿化工程是造福子孙后代的大事。确定在一定条件下栽树、种花的棵数是最简单、最基本的“植树问题”。还有许多应用题可以化为“植树问题”来解,或借助解“植树问题”的思考方法来解。
一.四类最简单、最基本的植树问题
为使其更直观,我们用图示法来说明。树用点来表示,植树的沿线用线来表示,这样就把植树问题转化为一条非封闭或封闭的线上的“点数”与相邻两点间的线的段数之间的关系问题。
显然,只有下面四种情形:
(1)非封闭线的两端都有“点”时,
“点数”=“段数”+1。
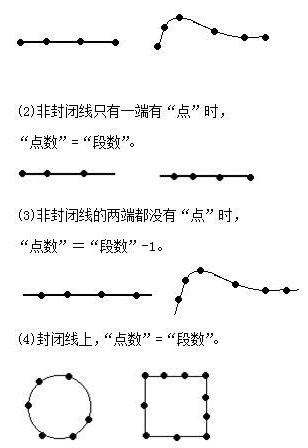
最简单、最基本的植树问题只有这四类情形。
例1.一条河堤长420米,从头到尾每隔3米栽一棵树,要栽多少棵树?
【解析】这是第(1)种情形,所以要栽树420÷3+1=141(棵)。
例2.肖林家门口到公路边有一条小路,长40米。肖林要在小路一旁每隔2米栽一棵树,一共要栽多少棵树?
【解析】由于门的一端不能栽树,公路边要栽树,所以,属于第(2)种情形,要栽树40÷2=20(棵)。
例3.两座楼房之间相距30米,每隔2米栽一棵树,一直行能栽多少棵树?
【解析】因紧挨楼房的墙根不能栽树,所以,属于第(3)种情形,能栽树30÷2-1=14(棵)。
例4.一个圆形水池的围台圈长60米。如果在此台圈上每隔3米放一盆花,那么一共能放多少盆花?
【解析】这属于第(4)种情形,共能放花60÷3=20(盆)。
综上所述,在许多应用题中都可以借助或归结为上述植树问题求解。
二.植树问题的应用
例1.在一段路边每隔50米埋设一根路灯杆,包括这段路两端埋设的路灯杆,共埋设了10根。这段路长多少米?
【解析】这是第(1)种情形,所以,“段数”=10-1=9。这段路长为50×(10-1)=450(米)。
答:这段路长450米。
例2.小明要到高层建筑的11层,他走到5层用了100秒,照此速度计算,他还需走多少秒?
【解析】因为1层不用走楼梯,走到5层走了4段楼梯,由此可求出走每段楼梯用100÷(5-1)=25(秒)。走到11层要走10段楼梯,还要走6段楼梯,所以还需25×6=150(秒)。
【解析】[100÷(5-1)]×(11-5)=150(秒)。
答:还需150秒。
例3.一次检阅,接受检阅的一列彩车车队共30辆,每辆车长4米,前后每辆车相隔5米。这列车队共排列了多长?如果车队每秒行驶2米,那么这列车队要通过535米长的检阅场地,需要多少时间?
【解析】车队间隔共有30-1=29(个),每个间隔5米,所以,间隔的总长为(30-1)×5=145(米),
而车身的总长为30×4=120(米),故这列车队的总长为(30-1)×5+30×4=265(米)。由于车队要行265+535=800(米),且每秒行2米,所以,车队通过检阅场地需要(265+535)÷2=400(秒)=6分40秒。
答:这列车队共长265米,通过检阅场地需要6分40秒。
例4.下图是五个大小相同的铁环连在一起的图形。它的长度是多少?十个这样的铁环连在一起有多长?

【解析】如上图所示。关键是求出重叠的“环扣”数(每个长6毫米)。根据植树问题的第(3)种情形知,五个连在一起的“环扣”数为5-1=4(个),所以重叠部分的长为6×(5-1)=24(毫米),
又4厘米=40毫米,所以五个铁环连在一起长40×5-6×(5-1)=176(毫米)。同理,十个铁环连在一起的长度为40×10-6×(10-1)=346(毫米)。
答:五个铁环连在一起的长度为176毫米。十个铁环连在一起的长度为346毫米。
例5.父子俩一起攀登一个有300个台阶的山坡,父亲每步上3个台阶,儿子每步上2个台阶。从起点处开始,父子俩走完这段路共踏了多少个台阶?(重复踏的台阶只算一个)。
【解析】因为两端的台阶只有顶的台阶被踏过,根据已知条件,儿子踏过的台阶数为300÷2=150(个),
父亲踏过的台阶数为300÷3=100(个)。由于2×3=6,所以父子俩每6个台阶要共同踏一个台阶,共重复踏了300÷6=50(个)。所以父子俩共踏了台阶150+100-50=200(个)。
答:父子俩共踏了200个台阶。
以上是《国家公务员考试之行测重要考点:植树问题》的全部内容,更多资讯请继续查看:甘肃省考考试网(https://gs.huatu.com/)
(编辑:shirui)
华图教育兔小妹

甘肃华图微信公众号
下一篇:没有了